理論化学
化学講座 第38回:飽和蒸気圧
温度と熱運動のはげしさ
コップに水を入れておき、それを放置しておくと、いつの間にか水が乾燥してなくなっています。しかし、コップにしっかりとふたをしておくと水はなくならず、いつまでもそのままの状態です。
この現象を、分子の挙動に着目して考えてみましょう。液体を構成している分子は熱運動と分子間力がちょうど釣り合ったような状態であるという話は以前にしましたね。蒸発というのは、分子の熱運動が分子間力を上回った時に起こる現象で、分子が分子間力を断ち切って液体中から飛び出し、気体になる事です。
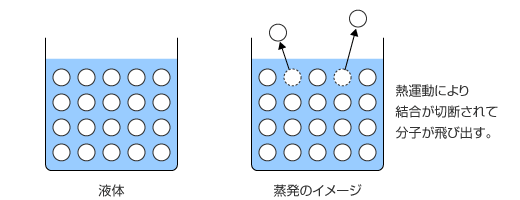
さて、分子の熱運動は温度が高いほど激しくなりますが、同じ温度ならどの分子も同じ激しさで運動しているというわけではなくて、ものすごく激しく運動しているものもあれば、ものすごくゆるやかに運動しているものもあります。
つまり、温度が高く気体分子の熱運動が激しいというのは、気体分子の熱運動の激しさの平均値が大きいという意味です。
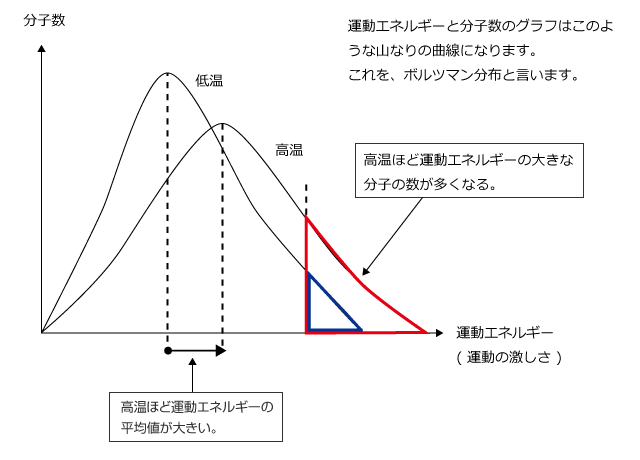
液面近くの分子で熱運動が分子間力を上回るような分子は、分子間力を断ち切って液面から飛び出していきますが、温度が高いほどこのような分子の割合が増えますから、蒸発速度は温度が高いほど大きくなるのです。
蒸発速度と凝縮速度・飽和蒸気圧
一方、気体になった分子が液体の表面に衝突するとどうなるでしょうか。衝突した分子の一部は跳ね返されて気体のまま残りますが、そうでない気体分子は分子間力に負けて液体にとりこまれる。つまり凝縮します。この凝縮速度は、圧力が高いほど大きくなります。理由は考えればなんとなくわかると思います。圧力が高い方が分子が衝突する頻度も衝突するときの速度も大きくなるわけですよね。頻度が高くたくさんぶつかる方が取り込まれる分子が増えるでしょう。また、大きな速度でぶつかるほど液体の内部にもぐりこみやすいだろう。と想像できますね。
蒸発速度・・・ 温度が高いほど大きくなる。
凝縮速度・・・ 圧力が高いほど大きくなる。
体積一定の容器を真空にして、その中に液体を入れて一定温度に保って放置します。すると最初は圧力は0 ですので凝縮速度は 0 、蒸発だけが起こります。
しかし、蒸発が起こって気体が生じ、圧力が高くなると凝縮も始まります。最初は蒸発速度>凝縮速度ですが、蒸発が進んで蒸発速度と凝縮速度が同じになった時、蒸発と凝縮がちょうど打ち消し合って、見かけ上蒸発も凝縮も起こらなくなります。この状態を気液平衡といいます。
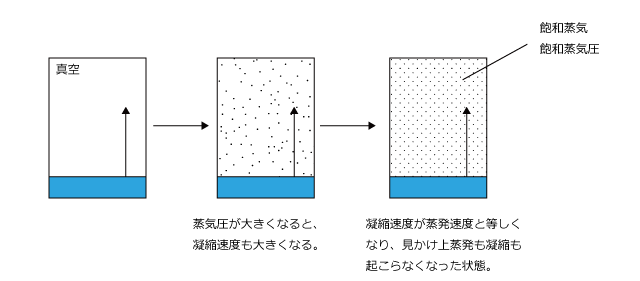
ある温度において気液平衡になった時の気体の圧力をその温度における飽和蒸気圧と言います。
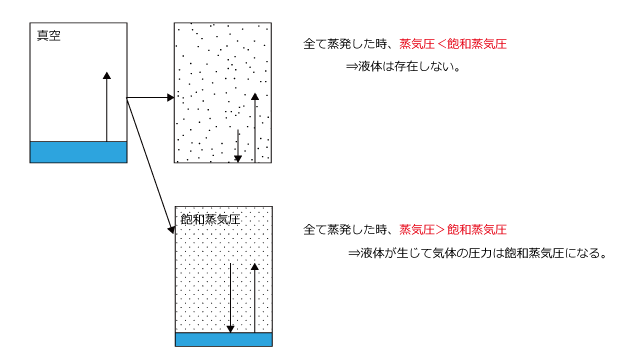
気体の圧力は飽和蒸気圧以上にすることは出来ません。なぜなら、蒸気圧が飽和蒸気圧より大きくなると、凝縮速度が蒸発速度を上回り、気体が凝縮して圧力が小さくなり、最終的に飽和蒸気圧になってしまうからです。
逆に気体の圧力が飽和蒸気圧に等しくなると気液平衡になる。ということは、飽和蒸気圧になる前に液体が全て蒸発してしまった場合はどうなるかというと、、気液平衡にならない状態(蒸発速度が凝縮速度を上回った状態)のまま、全て気体になって液体がない状態になります。
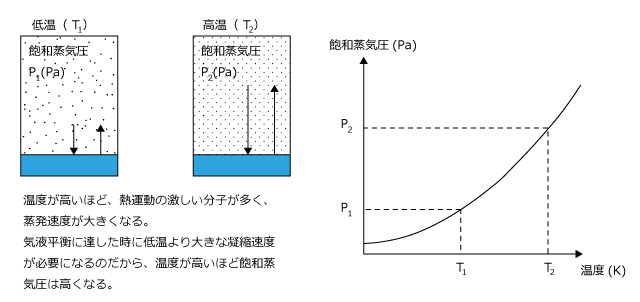
次に、温度と飽和蒸気圧の関係について考えてみましょう。
温度が高いほど蒸発速度が大きくなるのですから、温度が高いほど飽和蒸気圧も大きくなるわけです。飽和蒸気圧と温度の関係は下図のような曲線になり、この曲線を飽和蒸気圧曲線と言います。
おまけ:飽和蒸気圧曲線の求め方について
:ここは高校の範囲ではないので飛ばしてもかまいません。
※ 高校では、ポテンシャルエネルギーが減少する方向に進む。という事しか習いませんが、実は変化の方向は、このエネルギーの増減だけで決まるわけではないのです。例えば、塩化アンモニウムの水への溶解は吸熱反応(ポテンシャルエネルギーが増加する方向)であるにもかかわらず、水に塩化アンモニウムを加えると容易に溶解します。
これはポテンシャルエネルギーのほかにもう 1 つ、変化の方向を決めている要因があるからです。
それはエントロピーです。世の中はエントロピーの増大する方向に向かう、というのを聞いたことがあると思いますが、エントロピーとは乱雑さの度合いの事です。つまり、世の中はどんどん乱雑な方向に向かっていくという事なんですね。
分かりにくいと思いますので、例を出してみましょう。今下図のように水槽の中に黒玉を 10 個と白球を 10 個いれてこれを振り混ぜます。そうすると、白球と黒球はぐちゃぐちゃに混ざってしまって、どんなに振っても最初の状態には戻らないですよね。
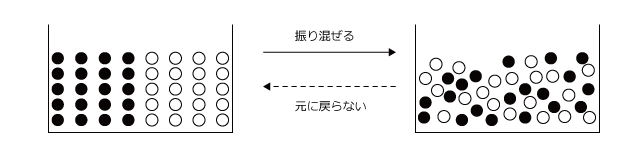
これは、最初の状態になる場合の数が、すべての場合の数に比べてとても小さいからなのです。このように、乱雑さの小さな状態は、大きな状態よりそうなる確率が無視できるくらい小さいという事です。
エントロピーとポテンシャルエネルギーに、気体が外部にする仕事を加えた値を自由エネルギーといいます。そして、自由エネルギーが減少する方向が自然に反応が進む方向です。(自由エネルギーの式の中ではエントロピーの前にマイナスがついていて、エントロピーが増加すると、自由エネルギーが減少するようになっている。)
さて、気液平衡の状態というのは、気体でも液体でもどっちでもいいという状態ですね。つまり、気体と液体の持っている自由エネルギーの大きさが同じになっている状態です。これを式にすると下のようになります。
( 1 mol の液体が持っている自由エネルギー )=( 1 mol の気体が持っている自由エネルギー )
この式を変形すると、温度 T(K) と蒸気圧 P(pa) の関係式が得られるのですが、その式が飽和蒸気圧と温度のグラフの式なのです。これを、クラジウス・クラペイロンの式と言います。
1 ) 飽和蒸気の温度を低下させた場合
ある温度の飽和蒸気圧になっている気体の温度を下げると、飽和蒸気圧が低下するため液体が凝縮します。凝縮はその温度での飽和蒸気圧になるまで続き、飽和蒸気圧に達すると気液平衡になってそれ以上液体は生じなくなります。
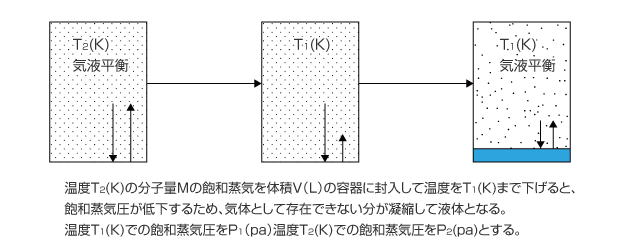
さて、上図の例でどれくらいの液体が凝縮するかを考えてみましょう。
気体の分子量をM、温度 ![]() 体積
体積 ![]() の飽和蒸気には
の飽和蒸気には ![]() の気体が含まれるとします。
の気体が含まれるとします。
すると、気体の状態方程式より
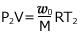 ・・・①
・・・①
次に、 での飽和蒸気圧を ![]() で、
で、![]() の液体が凝縮したとします。
の液体が凝縮したとします。
すると、気体は  存在しますから、気体の状態方程式より
存在しますから、気体の状態方程式より
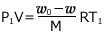 ・・・②
・・・②
が成立します。①、②で、![]() は勝手においた値ですから、これを消せば、
は勝手においた値ですから、これを消せば、![]() を得ることができますね。
を得ることができますね。
①より、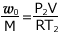 これを ② へ代入して、
これを ② へ代入して、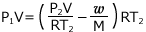
これを整理すると、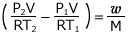 よって、
よって、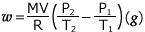 が得られます。
が得られます。
2 ) ある温度の気体に圧力を加えた場合
次は、温度 ![]() 圧力
圧力 ![]() 体積
体積 ![]() の気体に圧力を加えていった時に起こる現象を考えてみます。ただし、
の気体に圧力を加えていった時に起こる現象を考えてみます。ただし、![]() は
は ![]() での飽和蒸気圧より小さいものとします。
での飽和蒸気圧より小さいものとします。
最初は圧力が飽和蒸気圧より小さいため、蒸発速度>凝縮速度となって、全て気体の状態です。(図 ①)
次に、圧力を  まで上昇させると、蒸発速度は少し大きくなりますが、凝縮速度より小さいので、まだ全て気体です。(図 ②)
まで上昇させると、蒸発速度は少し大きくなりますが、凝縮速度より小さいので、まだ全て気体です。(図 ②)
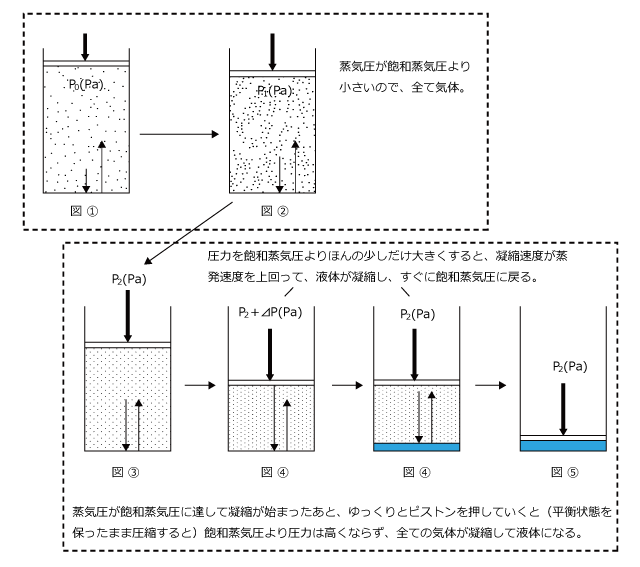
さらに圧力を加えて、蒸気圧が飽和蒸気圧 ![]() になると気液平衡に達する (図 ③)。ここで、もう少しだけピストンを押し込むと (図 ④) 圧力が飽和蒸気圧を越えて蒸発速度より凝縮速度が上回ります。
になると気液平衡に達する (図 ③)。ここで、もう少しだけピストンを押し込むと (図 ④) 圧力が飽和蒸気圧を越えて蒸発速度より凝縮速度が上回ります。
すると、凝縮が起こって気体の物質量が減少して蒸気圧が低下し、すぐに飽和蒸気圧![]() で気液平衡になります。(図 ④)このように、ピストンに圧力をゆっくりと加えていくと、凝縮が起こった時点からはずっと飽和蒸気圧のまま全て液体になります。(図 ⑤)
で気液平衡になります。(図 ④)このように、ピストンに圧力をゆっくりと加えていくと、凝縮が起こった時点からはずっと飽和蒸気圧のまま全て液体になります。(図 ⑤)
3 ) ある温度の飽和蒸気を圧縮した場合
温度 ![]() 、体積
、体積 ![]() 、圧力
、圧力 ![]() の飽和蒸気を圧縮して
の飽和蒸気を圧縮して ![]() にします。すると、蒸気圧は飽和蒸気圧を超えるので、凝縮速度>蒸発速度となって凝縮が起こります。
にします。すると、蒸気圧は飽和蒸気圧を超えるので、凝縮速度>蒸発速度となって凝縮が起こります。
凝縮が起こると蒸気圧は低下しますが、蒸気圧が飽和蒸気圧の ![]() になると再び気液平衡となって、見かけ上、凝縮も蒸発も起こらなくなります。こうやって外界から変化を与えると、変化を与えた直後は平衡とは違う状態になるのですが、しばらく時間が経過すると結局は気液平衡の状態になってしまうのです。
になると再び気液平衡となって、見かけ上、凝縮も蒸発も起こらなくなります。こうやって外界から変化を与えると、変化を与えた直後は平衡とは違う状態になるのですが、しばらく時間が経過すると結局は気液平衡の状態になってしまうのです。

では、この過程でどれくらいの量の液体が得られたのかを考えてみましょう。図 ① の気体には![]() の気体が入っており、図 ③ では
の気体が入っており、図 ③ では ![]() の液体が得られたとします。気体の分子量は M とします。
の液体が得られたとします。気体の分子量は M とします。
図 ① では、理想気体の状態方程式より、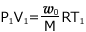 ・・・ ①
・・・ ①
図 ② では、理想気体の状態方程式より、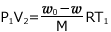 ・・・ ②
・・・ ②
①式より、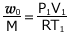 これを②式に代入して、
これを②式に代入して、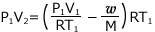
これを整理すると、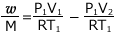 よって、
よって、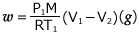 となるわけです。
となるわけです。
4 ) 化学反応によって、凝縮する気体が生じる場合
温度 ![]() 、体積
、体積 ![]() の容器の中に、物質を入れて反応させた時、生じる気体が凝縮する可能性があるような問題を考えてみましょう。例えば、
の容器の中に、物質を入れて反応させた時、生じる気体が凝縮する可能性があるような問題を考えてみましょう。例えば、![]() と
と ![]() が反応して、
が反応して、![]() が生じるような問題です。
が生じるような問題です。
このとき、反応後、実際に液体が生じるかどうかを判断するには、生じた物質が全て気体であると仮定して圧力を計算して、その値が飽和蒸気圧より大きいか小さいかを比較します。
飽和蒸気圧以下であった場合は、液体は生じません。
逆に、飽和蒸気圧より大きかった場合、液体が生じ定飽和蒸気圧になるまで液体が凝縮します。
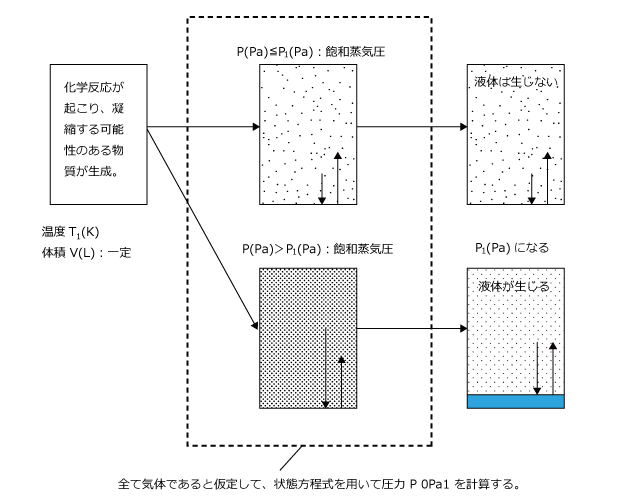
P(Pa) ≦ P1(Pa) の時:液体は生じず、全て気体のまま存在する。
P(Pa) > P1(Pa)の時:液体が生じて圧力は P1(Pa) になる。
液体が生じる場合、生じた液体の量は3)と同じようにして求めます。