溶解度が小さく、溶媒と反応しない気体を一定温度、一定体積の溶媒に溶解するとき、溶解する物質量はその気体の分圧に比例します。これをヘンリーの法則といいます。

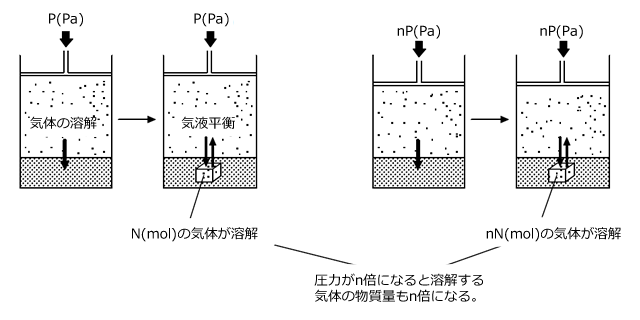
このヘンリーの法則には、もう１つ書き方があって、それは溶解度が小さく、溶媒と反応しない気体を一定体積の溶媒に溶解するとき、溶解する気体の体積は圧力によらず一定である。というものです。一見矛盾したことを言っているように思えますね。

これを説明するために、まずN(mol)の気体に着目しましょう。

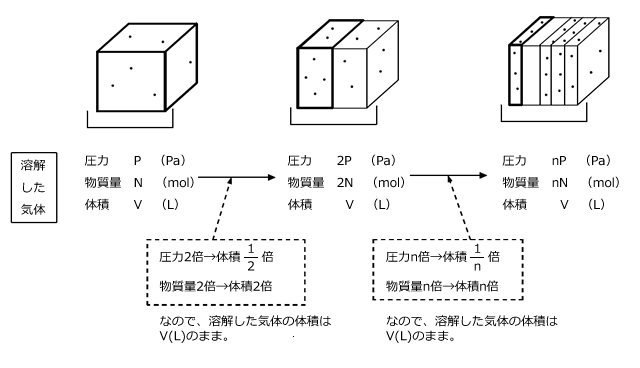
N(mol)の気体がP(Pa)のとき、V(L)を占めたとします。では、この圧力が2P(Pa)になったらどうでしょうか。 当然、体積はの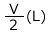となります。圧力がnP(Pa)になると、体積はの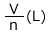となります。

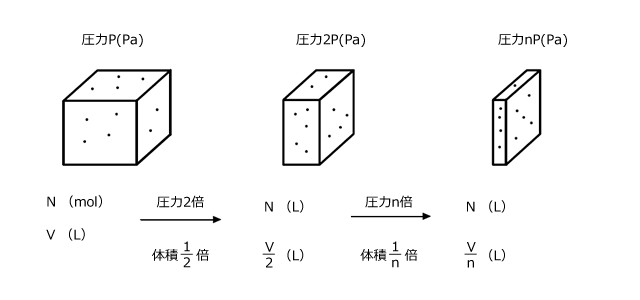
このように、物質量が一定であれば圧力が高くなればなるほど、それに反比例して体積は小さくなっていきます。

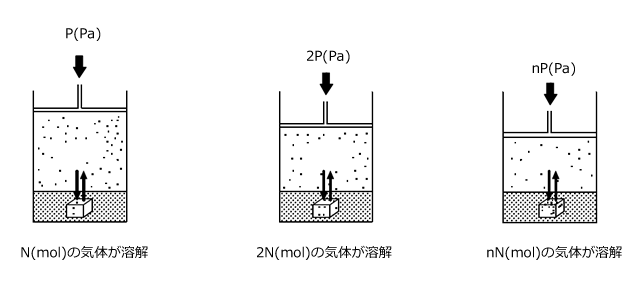
一方で、最初に説明したように、圧力に比例して液体に溶解する気体の物質量は増加します。

すると、圧力が増加すると、圧力に反比例して気体の体積が減少し、一方で圧力に比例して気体の物質量が増加します。結局、この二つの影響が打ち消し合って、各圧力において溶解する気体の体積は等しくなるのです。

ちなみに、気体の溶解度は温度が高くなるほど小さくなります。これは気体の溶解が発熱反応であるため、後述するルシャトリエの原理により、温度が高くなるほど気体が生じる方向に平衡が偏るためです。

ヘンリーの法則の頻出問題

最後に、ヘンリーの法則関連の問題で、難易度が高く、出題頻度も比較的高い問題の解き方を説明しておこうと思います。まず、体積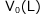の容器に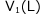の液体を入れます。この液体は蒸発しないものとします。次に、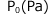で1(L)のこの液体に、N(mol)溶解する気体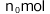を封入する。実験はT(K)で行われたとします。十分時間が経過した後、この気体の圧力と溶解している気体の物質量を求めなさい。
という問題です。

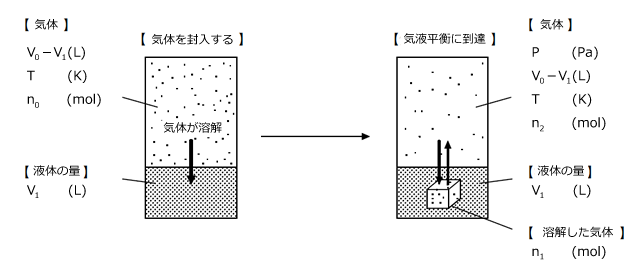
十分時間が経って気液平衡に達したときの気体の圧力をP(Pa)、液体に溶解した気体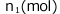、気体のまま残ってるものを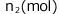とします。

3つの未知数をおきましたから、3つの方程式が必要ですね。では、どのような式が成立するか考えてみましょう。

まず、気体部分について、状態方程式が成立します。次に、気液平衡なので、ヘンリーの法則が成立します。

最後に、溶解した気体の物質量と気体のまま存在している物質量の和は最初に封入した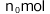に等しいという式（物質量保存の式）が成立します。

①　気体の状態方程式　
②　ヘンリーの法則　
③　物質量保存則　

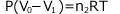
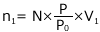
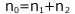
これらを解けば、Pとを求めることができます。
まず、Pを求めます③を用いてとを消去しましょう。

①より、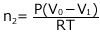　②より　これらを③へ代入します。

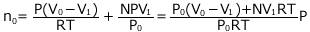これを解いて、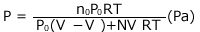

②へ代入して、