ここまでは、どのような化学反応が起こるか、ということに絞ってきました。
しかし、たとえ有益な化合物が得られる反応だったとしても、十分な量を得るのに長い時間がかかりすぎるのであれば、その反応は工業的には意味がありません。逆に、反応速度が速すぎると、短い時間に大量の熱が発生してしまい、最悪の場合、爆発事故が起こってしまうような場合もあります。
このようなことから、化学反応を取り扱う時には、反応速度について着目することも必要です。

今回は、不可逆反応の反応速度の定義や代表的なグラフについて説明します。

【( 平均の ) 反応速度 】：着目する物質の単位時間当たり、単位体積における物質量の変化の大きさ ( 着目する物質の単位時間当たりの濃度変化 )

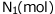ちょっとピンときませんね。そこで、図を描いて考えてみましょう。今、V(L)の容器の中でAという物質が反応して、時刻からの間にから、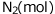へと変化したとします。この反応で反応速度を求めてみます。

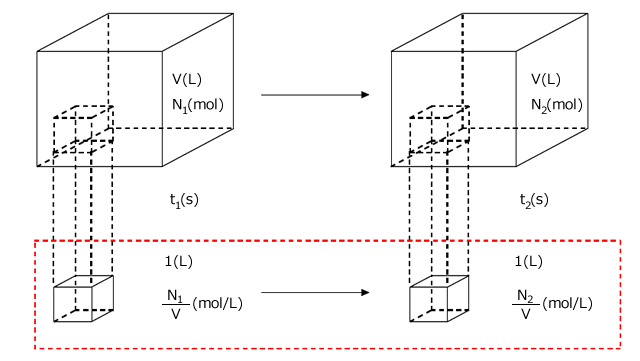
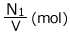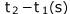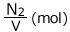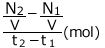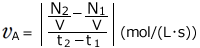
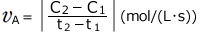1(L)あたりで考えます。V(L)の容器ですから、最初はあったものが後にになっていますね。1(s)あたり変化したことになります。化学反応速度はこの変化量の絶対値です。ですから、この反応における物質Aの反応速度はは体積モル濃度で、Cで表すと、と表せます。これが、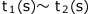の間のAの平均の反応速度です。

以上から、平均の反応速度＝着目する物質の単位時間当たりの体積モル濃度変化と言える事がわかりました。

では、反応速度はグラフ上でどのように表されるのか考えてみます。

横軸を時間(s)、縦軸を濃度(mol/L)とすると、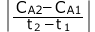は、このグラフ上の平均の速さ、つまり2点を結ぶ直線の傾きの大きさ(絶対値)、となります。

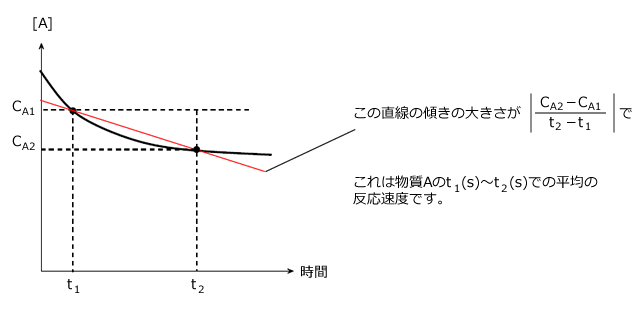
平均の速度があれば、瞬間の速度もあります。しかし、最初から瞬間を考えるのはちょっと大変そうです。
そこで、ある時刻t(s)における瞬間の反応速度を考える前にt(s)とそれからほんのわずかにずれた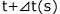での平均の反応速度を考えてみましょう。

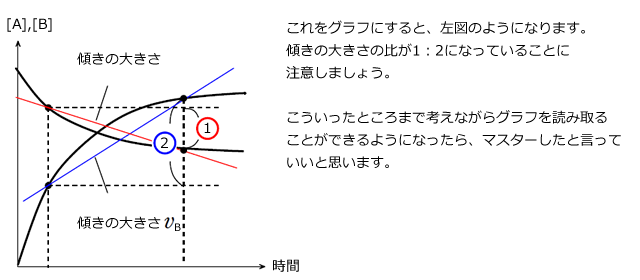
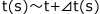での平均の反応速度は、下図左のように2点間を結ぶ直線傾きの大きさとして与えられます。ここで、を限りなく0にする。つまり、2点間を限りなく近づけると、下図右のように、2点間を結ぶ直線は時刻t(s)における接線となります。

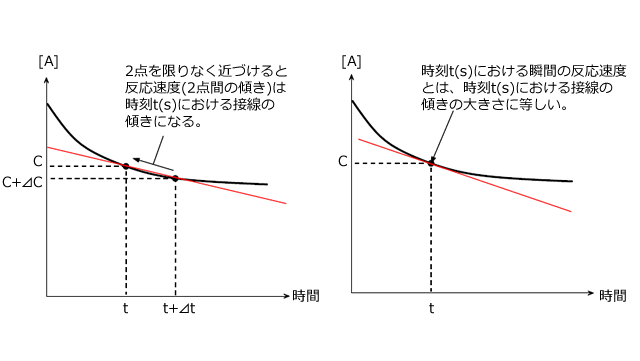
平均の反応速度＝時間-濃度グラフの 2 点を結ぶ直線の傾きの大きさ
瞬間の反応速度＝時間-濃度グラフのある点における接線の傾きの大きさ　と言えることが分かりましたね。

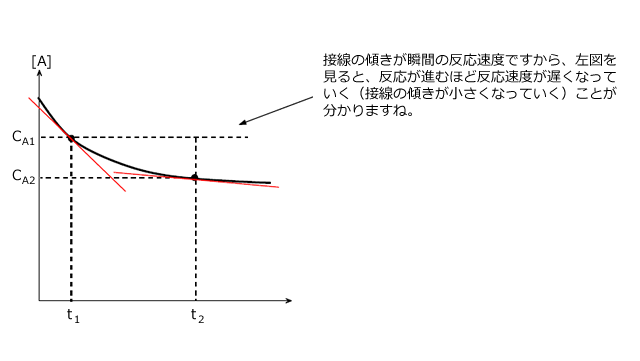
ここまでは、反応物に着目した反応速度を見てきました。では、生成物に着目した反応速度はどうでしょうか。

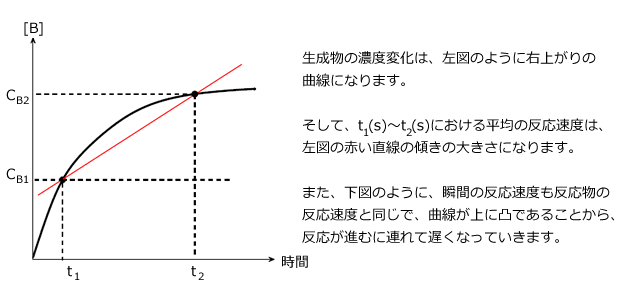
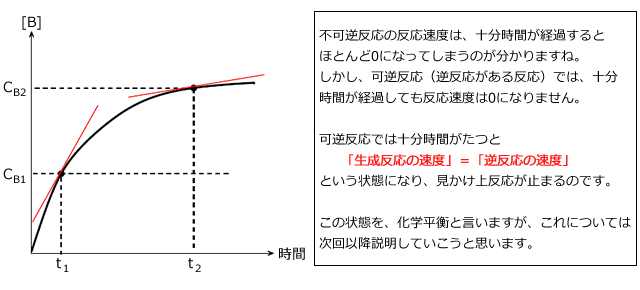
では、次に着目する物質によって反応速度が変化するかどうかを考えてみましょう。
例として、A→2Bで表される化学反応を容積一定の反応容器で反応させた場合を考えてみます。
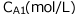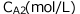この反応で、からの間に、Aの濃度がからに変化したとします。
すると、Aの反応速度は、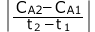(mol/(L・s))ですね。

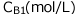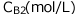一方、Bの濃度はからに変化したとします。

すると、Bの反応速度は、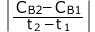(mol/(L・s))となります。

さて、AとBの反応速度の分母は同じ値ですね、ですから、この反応速度を比較するには、分子について比較すればいいことが分かります。分かりやすくするために表を書いてみましょう。

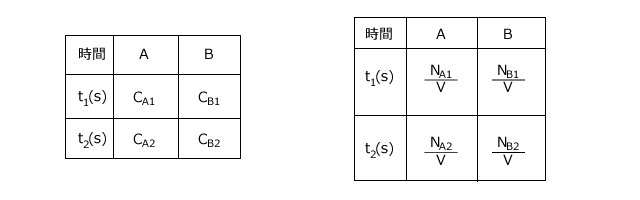
濃度変化だとぴんと来ないとおもうので、反応容器の体積をV(L)、物質量を(mol)、(mol)、(mol)、(mol)として、体積と物質量に直したものを描いておきました。

さて、すると、、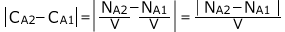

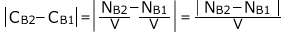となりますね。

さて、ここで、A→2Bという反応式は、1個のAが反応すると、2個のBが生成するという事を表しています。
従って、Bの増加量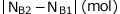はAの減少量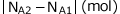の2倍です。

よって、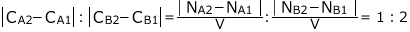

ですから、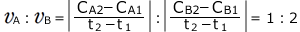
となります。

A→B2で表される化学反応速度は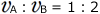となりましたが、係数が他の数字でも同じで
「化学反応速度の比」＝「化学反応式の係数の比」となります。